A very good friend of mine (let’s call him Jack) is a maths teacher.
A few weeks ago, after a particularly uninspiring training day at school, Jack was bemoaning the fact that maths teachers always have to ‘endure’ (his word, definitely not mine) training about literacy: literacy best practice, literacy across the curriculum, how to encourage reading in your lesson... The list went on.
But how often do other teachers have to consider how to teach numeracy in their classes? Jack pondered.
I wonder, do other maths teachers share his frustration? The conversation moved on, but I’ve been thinking about it recently, particularly about how academic vocabulary is taught in maths, about what language learning looks like in a maths classroom, and how the most effective maths teachers approach this area of their practice.
When young children learn language, words act as labels that signify objects that they are experiencing. When objects are visible or tangible, this is a relatively straightforward process. But when we are teaching students the names of abstract mathematical concepts, words describe processes that often lack a visual counterpart, and this can be tricky! Indeed, a quick scan of the new AQA higher maths paper reveals many of these fairly abstract ideas: Integer, probability, the nth term, to name but a few.
But why is it important that a student knows this vocabulary? Many maths teachers would argue that what you call a process doesn’t matter too much if you are able to perform that process effectively. However, research suggests that a sound understanding of maths vocabulary is inextricably linked to a student’s conceptual understanding of mathematics (Capraro, Capraro, and Rupley 2010; Capraro and Joffrion 2006; Kotsopoulos 2007).
We acquire most of our vocabulary incidentally through indirect exposure to words, in the books we read, the films we watch and the conversations we have, but maths vocabulary is highly decontextualised. Unless you work in a maths related field, ‘integer’ or ‘nth term’ doesn’t pop up in conversation that often. While teachers of other subjects might be able to rely on learners picking up language along the way (they shouldn’t – more of that here…) maths teachers don’t have that luxury. If you’re not teaching it, your students probably aren’t learning it.
So what are the key things to think about when teaching new maths terms?
1. Pre-teaching new language
When you teach a new word at point-of-use, the word can be lost or misunderstood as learners struggle with a new concept. To take ‘probability’ as an example, start learners off by explaining that the new word is a noun and it is the name we give to the likelihood of something happening.
Starting off with the target vocabulary gives learners something to attach new abstract concepts to, as and when you introduce them. Then, as you move through the following steps, their understanding of the new term (and concept) will become increasingly nuanced.
2. Develop nuanced understanding
If you want to help learners develop a more nuanced understanding of terms and their characteristics, here are some ideas to try:
The Frayer model: When defining an abstract concept, it is useful to think about what that idea IS and IS NOT. The Frayer model encourages learners to think about the defining characteristics of a concept.
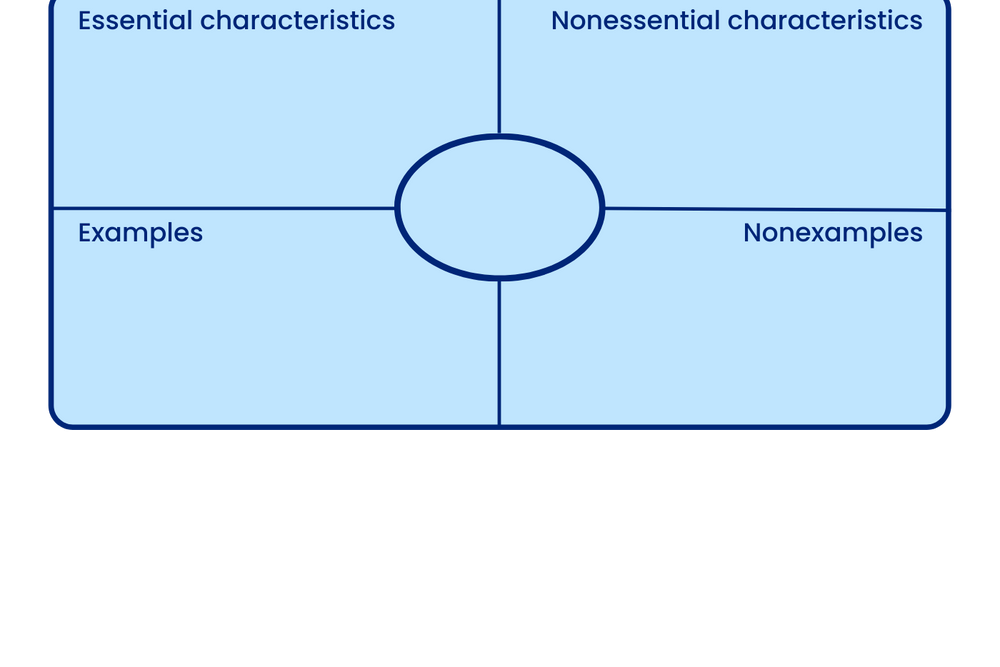
So, to take ‘Prime Numbers’ as an example, essential characteristics include the fact that a prime number has exactly two positive divisors, 1 and the number itself. Non-essential characteristics include the observation that prime numbers are usually odd.
Once you’ve introduced the new word and the new concept, try using this step-by-step guide to improving understanding. It’s inspired by an American researcher called Robert Marzano and I think it could work just as effectively in a maths classroom as an English classroom.
Step 1: Explain
- This should be in language the students are familiar with. Providing examples from their own lives will help. Research has shown that when students learn a teacher’s definition of a word, learning is less effective. Don’t get them to record anything at this stage. Wait until…
Step 2: Reinstate
- Ask learners (in pairs or groups) to explain to each other what the word means and create examples of the word in use. Take feedback and correct where necessary, then ask learners to make a note of their understanding of the word.
- (This would be a good point to introduce the concept behind the new term. After which, you can use the following steps to assess learners’ comprehension and to encourage them to develop a more nuanced understanding.)
Step 3: Show
- This is the bit that really deepens understanding and for you as a teacher, quickly highlights which learners haven’t quite understood. Ask learners to draw a picture, a symbol or some form of graphic representation of the term. Encourage learners to explain why they have depicted the term in that way.

Subject-specific vocabulary with Bedrock Mapper
Encourage every learner to communicate like an expert in every subject across the curriculum.
Step 4: Discuss
- Try using a structured discussion to ‘flesh out’ learners' understanding of the new term. Ask learners in groups to come up with synonyms and antonyms of the word. For example, a synonym for probability might be ‘likelihood’ or ‘chance.’ Then, ask learners to devise metaphors or analogies for that word. So, for example if the word was ‘evaluate,’ a metaphor might be ‘evaluate is an estate agent telling you how much your house is worth.’
Step 5: Refine and reflect
- Go back to their exercise book and look at their original note (Step 2). Ask learners to see if they want to make any changes to their original idea. Encourage learners to share revisions with the class and explain why they made the changes they did.
Step 6: Play!
- By now, learners should have a pretty nuanced understanding of the new mathematical terms so it’s time for the games to begin! Charades, taboo, bullseye, jeopardy, anything goes. These games are all designed to encourage students to think about the qualities of words and it should be really interesting to see how students interpret the abstract concepts.
By teaching mathematical vocabulary as well as mathematical concepts, you are promoting conceptual understanding amongst learners. By supporting their acquisition of mathematical language, you are helping them to read and interpret problems successfully and as Cobb (1998) suggests, as children develop mathematics language, they learn to communicate and share universal mathematical concepts and operations with their peers and others.
If you are a maths teacher, we would love to hear from you. Please do share your experiences with us and let us know how the language of maths is taught in your classroom!




